⏳ Mining deep into Data Mining - Statistics - PART II ⏳

 Before analyzing distributions in statistics, Let's understand the required essential basics

💭 MEAN

Mean is an essential concept in statistics. In common terms, it can be defined as the average of a collection of values. It can be referred to as central tendency or centrality for a probability distribution. Thus, it basically denotes the centrality of a series of values.

💭 STANDARD DEVIATION

A standard deviation is a statistic that measures the dispersion of a dataset relative to its mean. The standard deviation is calculated as the square root of variance by determining each data point's deviation relative to the mean.

💭 VARIANCE

Variance is the measure of how well the data is dispersed from the existing data points. (ie) the mean squared difference between every data point and the center of distribution (mean). This yields the rate of dispersion of data points. Variance is also the square of standard deviation.

For example, let's consider a series of price list values of multiple products in a supermarket.

price_list = [87.56, 56.78, 98.76, 56.43, 32.12, 76, 90, 43.45, 76.23, 12.05]

Mean = sum of price_list / number of entries in price_list

                                    MEAN = SUM(price_list) / LEN(price_list)

Variance = for each value v in the list, perform square of the difference between the element and the mean (ie) square of (v - mean), finally perform a summation

                          VARIANCE = SUM(square of (v - mean) for every v in price_list) / LEN(price_list)

Standard deviation = Perform the square root of the variance 

                                        STD = SQRT(variance)


Let us assume, the height of 5 dogs are calculated. (Reference & Image Source: Internet)

               👉 The GREEN line represents the mean or average height of the dogs.

              👉  The difference between the INVERTED RED indicator and the mean denotes the variance. 

               👉 The square root of the variance (would be less than the variance) - the BLUE line is the threshold value, thus the standard deviation would be the square root of the sum of the difference of every value against the total values (ie) the square root of variance. 

Let's understand what distribution is all about 💪

DISTRIBUTION

A distribution in statistics is a function that shows the possible values for a variable and how often they occur. Let's assume a die numbered from 1 to 6. When rolling the die, there are possibilities that values from 1 to 6 might appear on the dice. Thus, the distribution of an event consists not only of the input values that can be observed but is made up of all possible values.

Based on the type of data being dealt with, there are two different types of distribution - Discrete and Continuous distribution. 

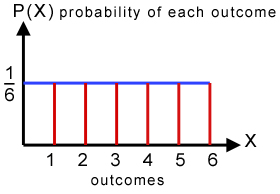
👉 DISCRETE UNIFORM DISTRIBUTION - Outcomes are likely to be equal

In simple terms, uniform distribution refers to cases where the outcomes are likely to be equal. Let us consider the scenario of rolling a die, there is an equal possibility of the values 1, 2, 3, 4, 5, and 6 appearing in the next throw. Thus, the probability is 1/6 or 0.16666. 

The figure below shows the equal likeliness of the outcomes (Image Source: Internet)

👉 BERNOULLI DISTRIBUTION - Two outcomes for every trial.

Bernoulli Distribution is very simple and indeed the inception of many complex distributions. Let's say we flip a coin once (ie) a single trial, and there are two possible outcomes - Head or Tail. 

Mathematically, Bernoulli distribution can be represented as, for every outcome p, the total probability is (1) - in which one is p and the other is 1-p. The figure below shows the outcome distribution: true and false which could be represented as p (1) and (1-p). (Image Source: Internet)


👉 BINOMIAL DISTRIBUTION - Series of Bernoulli trials

In simple terms, Binomial distribution can be viewed as the sum of the outputs of a single trial in a Bernoulli distribution event. For example, a coin flip event is made multiple times to determine the head and tail count.

 The figure below shows the distribution of multiple trials (dotted green, blue, and red)  undertaken to infer the probable outcome. (Image Source: Internet)


👉 NORMAL DISTRIBUTION - A continuous distribution that distributes values around the mean

 It is one of the most commonly used distributions in data science. To simply describe the normal distribution, the continuous range of values has a peak at the mean, and then taper off as they move away from the center point. Thus, the shape of the graph would be in a bell fashion or say bell curve.  

The reason I feel this has got the specific term (Normal) is that there are many real-life natural scenarios that concur with the distribution pattern. For example, the height of a person as he ages, stock market growth, birth weight of a kid, the shoe size of a person etc..

The below figure shows a simple representation of normal distribution as the peak of the value occurs at the central point and then turns down as it moves away from the mean or center (Image Source: Internet)



👉 STUDENT'S T-TEST DISTRIBUTION - Similar to a normal distribution with a small sample size

It is mostly similar to the normal distribution with a bell-shaped curved - but used in cases the initial sample size is small. 

For example, to understand better, we could use a normal distribution in cases when we have to determine the supplies sold in a departmental store. We could use T-Test distribution to determine the sales made in a day in the same departmental store. It is generally used in hypothesis testing with limited sample data

The below figure shows the T-distribution that looks similar to the normal distribution but there exists no central value (mean) as a threshold.



We have discussed five predominantly used distributions in data science and data mining tasks. There are several other distributions in statistics that widely serve as the primary hypothesis to infer many other principles and proofs. These distributions form the basis of statistical and probability analysis that in turn is applied using advanced python libraries to ease our implementations.

                                    💡 Let's keep mining deeper  !!! 💡


Comments

Post a Comment

Articles by Hemapriya

Comprehending the state-of-art Digit Recognizer dataset using machine learning

Image
   Handwriting Recognition Handwritten text recognition has been a challenge since the first automatic machines were required to identify individual characters in handwritten texts.Consider the five-digit ZIP codes on letters at the post office and the automation used to identify them.To sort mail automatically and efficiently, perfect understanding of these codes is required. Included among the other applications that may come to mind is OCR (Optical Character Recognition) software. OCR software must read handwritten text, or pages of printed books, for general electronic documents in which each character is well defined. But the problem of handwriting recognition goes farther back in time, more precisely to the early 20th Century (1920s), when Emanuel Goldberg (1881–1970) began his studies regarding this issue and suggested that a statistical approach would be an optimal choice.  To address this issue in Python, the scikit-learn library provides a good example to better...
Read more

Performance Analysis of Weather Data using Machine Learning

Image
   Weather and Climate Observations Weather data is primarily important for determining the climate of a region. Climate is determined by a number of factors.The formation and advancement of storm systems, the amount of precipitation an area gets, and the number of cloudy days are all influenced by air pressure, temperature, and humidity at various altitudes.These influences affect the environment on a local, international, and global scale over time. Why performance analysis of weather data is important ? The value of weather data analytics in human life is immense. Accurate weather forecasting is beneficial to the agricultural industry, tourism, and preparing for natural disasters such as floods and droughts. Weather forecasting has a lot of economic appeal in news organisations, government agencies, and industrial agriculture. Performance analysis of meteorological data: we can use weather and climate datasets to better understand and forecast the effect on shipping an...
Read more

💡⏳ Mining deep into Data Mining - PART II ⏳💡

Image
 Hurray💥 , we have seen the basics of data mining in Part I 😃 Let's get into the phases involved in the KDD process step by step. To start with, let's explore the Data Preprocessing phase. What actually is DATA in data mining? 🤔 In data mining, Data refers to the collection of objects and their attributes . Umm, Confusing right? 😨 👉 An Object is just like an entry in a table or an instance. It is also known as record, point, entity or sample. 👉 Attribute is any property or characteristic of an object. 👉 For example, If the eye of a person is considered as an object then, the eye color, blink rate are regarded as the attributes.  👉 Attribute can also be called a feature, field, characteristic, or variable in data mining. 👉 Here, the organization of data is in a tabular form.                                           ...
Read more